Introduction to Modelling Volatility and Correlations
While univariate GARCH models focus on modeling the volatility of a single asset, multivariate GARCH (MGARCH) models extend this framework to model the volatility and correlations between multiple assets. This is crucial for many financial applications, such as portfolio optimization, risk management, and asset pricing, where understanding the relationships between assets is essential.
The Importance of Modeling Correlations
- Portfolio Diversification: Correlations play a key role in portfolio diversification. Combining assets with low or negative correlations can reduce overall portfolio risk.
- Risk Management: Correlations are essential for calculating portfolio Value at Risk (VaR) and Expected Shortfall (ES). Underestimating correlations can lead to underestimation of portfolio risk.
- Asset Allocation: Correlations influence optimal asset allocation decisions. Investors may adjust their asset allocations based on changing correlation patterns.
- Derivatives Pricing: Correlations are important for pricing multi-asset derivatives, such as basket options and correlation swaps.
- Systemic Risk: Understanding correlations between financial institutions is important for assessing systemic risk and preventing financial crises.
Challenges in Modeling Volatility and Correlations
Modeling volatility and correlations in a multivariate setting presents several challenges:
- Curse of Dimensionality: The number of parameters to estimate increases rapidly with the number of assets. For example, a full covariance matrix for N assets has N(N+1)/2 unique elements. This can lead to estimation problems, especially with limited data.
- Positive Definiteness: The covariance matrix must be positive definite to ensure that portfolio variances are always non-negative. Imposing positive definiteness constraints on the model parameters can be challenging.
- Time-Varying Correlations: Correlations are not constant over time. They tend to fluctuate, exhibiting periods of high correlation (correlation clustering) and periods of low correlation.
- Asymmetric Effects: Correlations may respond asymmetrically to positive and negative shocks. For example, correlations may increase during periods of market stress.
- Computational Complexity: Estimating and forecasting with MGARCH models can be computationally intensive, especially for high-dimensional systems.
Traditional Approaches to Correlation Modeling
- Historical Correlations: Calculated as the sample correlations between historical returns. Limitations: Assume constant correlations, which is often unrealistic.
- Rolling Window Correlations: Calculated as the sample correlations over a rolling window of data. Limitations: More responsive to changing market conditions than historical correlations but still relatively simple and may not capture all the complexities of correlation dynamics.
- Factor Models: Model asset returns as a function of common factors. Correlations are induced by the common factors. Limitations: May not capture all the dependencies between assets.
Multivariate GARCH (MGARCH) Models
Multivariate GARCH (MGARCH) models provide a more sophisticated approach to modeling volatility and correlations by allowing the conditional covariance matrix to depend on past information. These models are particularly well-suited for capturing time-varying correlations and volatility clustering in a multivariate setting.
The general form of an MGARCH model is:

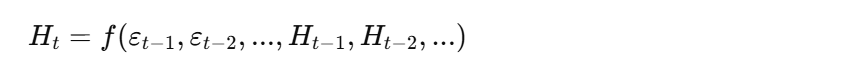
Where:
-
r_tis the vector of returns at time t -
μ_tis the conditional mean vector -
ε_tis the vector of error terms (or innovations) at time t -
H_tis the conditional covariance matrix at time t -
fis a function that specifies how the conditional covariance matrix depends on past error terms and past covariance matrices.
The challenge in MGARCH modeling is to specify the function f in a way that is both flexible enough to capture the key features of volatility and correlation dynamics and parsimonious enough to be estimable with available data.
Key Types of MGARCH Models
Several types of MGARCH models have been developed, each with its own strengths and weaknesses:
- VECH Model: The most general MGARCH model, but it has a very large number of parameters.
- Diagonal VECH Model: A restricted version of the VECH model that reduces the number of parameters by assuming that the conditional variances and covariances depend only on their own past values.
- BEKK Model: A parameterization that guarantees positive definiteness of the conditional covariance matrix.
- Constant Conditional Correlation (CCC) Model: Assumes that the conditional correlations are constant over time, while the conditional variances are time-varying.
- Dynamic Conditional Correlation (DCC) Model: Allows the conditional correlations to vary over time.
These models will be discussed in more detail in the following sections.
