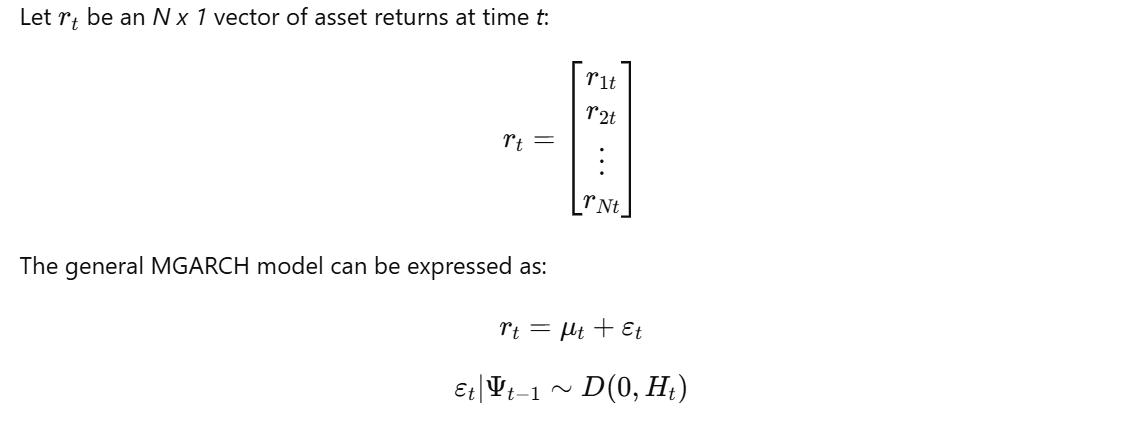Multivariate GARCH (MGARCH) Models
Multivariate GARCH (MGARCH) models are extensions of univariate GARCH models designed to model time-varying volatility and correlations between multiple assets. These models are crucial for capturing the intricate dependencies in financial markets and are commonly applied in portfolio optimization, risk management, and asset pricing.
General Framework
The general framework for MGARCH models involves defining a system of equations that describe the evolution of the conditional mean and the conditional covariance matrix for a vector of asset returns.
A key challenge in MGARCH modeling is choosing an appropriate functional form for ( H_t ) that is flexible enough to capture volatility and correlation dynamics while remaining parsimonious for estimation with available data.
Key Considerations in MGARCH Modeling
- Positive Definiteness: The conditional covariance matrix ( H_t ) must be positive definite to ensure non-negative portfolio variances. This is a critical requirement that must be met by the model specification.
- Parsimony: The model should aim for a relatively small number of parameters to prevent overfitting and ensure that the model can be estimated using available data.
- Interpretability: The model should be easy to understand and interpret.
- Computational Feasibility: The model should be computationally efficient to estimate and forecast, especially in high-dimensional systems.
Types of MGARCH Models
Several types of MGARCH models have been developed, each with its strengths and limitations:
- VECH Model: The most general MGARCH model but comes with a large number of parameters.
- Diagonal VECH Model: A simplified version of the VECH model that reduces the number of parameters by assuming that the conditional variances and covariances depend only on their own past values.
- BEKK Model: A parameterization that ensures the positive definiteness of the conditional covariance matrix.
- Factor MGARCH Models: Models the conditional covariance matrix as a function of a few common factors.
- Constant Conditional Correlation (CCC) Model: Assumes constant conditional correlations over time, while the conditional variances remain time-varying.
- Dynamic Conditional Correlation (DCC) Model: Allows the conditional correlations to change over time.
The VECH, Diagonal VECH, and BEKK models will be explored in more detail in subsequent sections.
Advantages of MGARCH Models
- Capture Time-Varying Volatility and Correlations: MGARCH models are designed to capture the time-varying volatility and correlations between multiple assets, making them highly valuable for understanding complex dependencies in financial markets.
- Enhance Risk Management: By providing accurate estimates of portfolio Value at Risk (VaR) and Expected Shortfall (ES), MGARCH models can significantly improve risk management strategies.
- Improve Portfolio Optimization: MGARCH models allow investors to account for time-varying correlations between assets, leading to better-informed portfolio optimization decisions.
Limitations of MGARCH Models
- Computational Complexity: Estimating and forecasting with MGARCH models can be computationally demanding, particularly in high-dimensional systems.
- Model Complexity: MGARCH models can be intricate and challenging to interpret.
- Data Requirements: Reliable parameter estimates typically require a large amount of data.
- Positive Definiteness Issues: Ensuring the positive definiteness of the conditional covariance matrix can be difficult and requires careful attention.
Conclusion
Multivariate GARCH (MGARCH) models are a powerful tool for modeling the volatility and correlations between multiple assets. These models are crucial for understanding the complex dependencies that arise in financial markets and are widely applied in portfolio optimization, risk management, and asset pricing. While MGARCH models offer significant advantages, they also present challenges such as computational complexity and the need for substantial data.