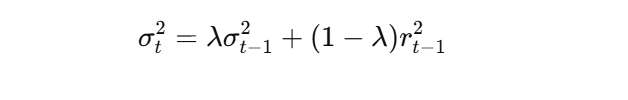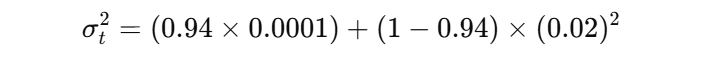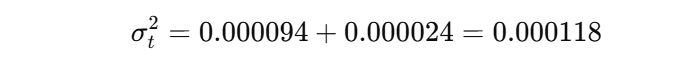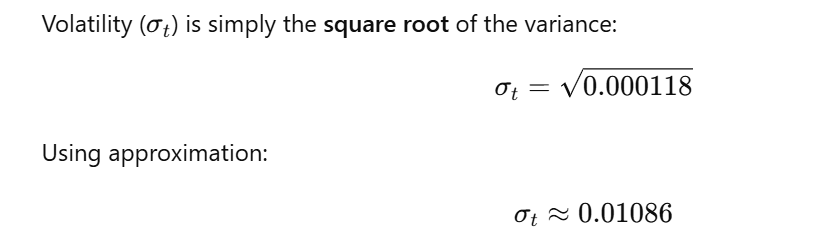Numerical Example

EWMA Volatility Calculation

Step 1: Given Data

Decay factor (λ): 0.94
Yesterday's estimated variance (σ²_{t-1}): 0.0001
Yesterday's return (r_{t-1}): 0.02 (2%)

We use the Exponentially Weighted Moving Average (EWMA) formula to update today’s variance:

Step 2: Substituting Values

Breaking it down:

( 0.94 \times 0.0001 = 0.000094 )
( (1 - 0.94) = 0.06 )
( (0.02)^2 = 0.0004 )
( 0.06 \times 0.0004 = 0.000024 )

Adding these values:

So, today's estimated variance is 0.000118.

Step 3: Compute Today's Volatility

Final Answer:
Today's estimated volatility is 1.086%.

Interpretation

Since yesterday's return (2%) was larger than yesterday's volatility (1%), today's estimated volatility has increased slightly.
The decay factor (λ = 0.94) controls how much weight is given to past volatility vs. recent returns:
- A higher λ (closer to 1) makes the model react slower to new shocks.
- A lower λ (closer to 0) gives more weight to the latest return, making volatility change faster.

Real-World Application

Financial risk management: Used in Value at Risk (VaR) calculations.
Stock market trading: Helps traders adjust their strategies based on recent market conditions.
Portfolio management: Used to dynamically adjust position sizes in response to changing market risk.

However, EWMA does not account for asymmetry in volatility (e.g., volatility tends to spike more after negative returns than positive ones). More advanced models like GARCH are often preferred for capturing these effects.

Would you like another numerical example, or is this clear? 🚀