Portfolio Analysis
Quantifying Performance and Risk
Portfolio analysis provides the tools to evaluate the effectiveness of a portfolio in achieving its objectives. The core elements are return and risk, and the key is to quantify these measures.
1. Portfolio Return
-
Explanation: This measures the overall performance of the portfolio, taking into account the returns of all individual assets and their respective weights.
-
Components Explained:
-
Rp: Portfolio Return -
Wi: Weight of asset i in the portfolio (expressed as a decimal) -
Ri: Return of asset i (expressed as a decimal) -
∑: Summation (addition) of the product of Wi and Ri for all assets in the portfolio.
-
-
Utility: Provides a single number summarizing the portfolio's overall performance over a specific period. It allows for comparison between portfolios.
-
Limitation This does not reflect the risks involved, nor what strategies were used in assembling the portfolio.
2. Portfolio Risk
-
Explanation: Measures the variability or uncertainty in the portfolio's returns. It quantifies the potential for losses. The book previously noted that an increase in the risk can increase potential return for an investment.
-
Decomposition of Risk:
-
Total Risk: Measured by Standard Deviation (σp) - Represents the overall volatility of the portfolio's returns.
-
Systematic Risk (Market Risk): Risk that affects the entire market and cannot be diversified away. It is inherent. In general, the greater amount of systematic risk involved, the greater chance for greater gains.
-
Unsystematic Risk (Company-Specific Risk): Risk that affects individual companies or industries. Can be reduced through diversification.
-
-
Formula for Portfolio Standard Deviation (Risk) - as provided:
- With:
-
Calculate the variance, which is standard deviation squared for each term.
-
The standard deviation of the assets cannot be simply summated to gain the standard deviation of the portfolio.
Components Explained:
-
σp: Portfolio standard deviation (a measure of total risk) -
Wi: Weight of asset i in the portfolio -
σi: Standard deviation of asset i (a measure of its individual risk) -
ρij: Correlation coefficient between assets i and j (a measure of how their returns move in relation to each other). You can have negatively and non-negatively correlated assets.
Interpretation:
- A higher portfolio standard deviation indicates greater volatility and, therefore, higher risk.
- The correlation coefficient (ρij) is important because it reflects how assets interact. A lower (or negative) correlation between assets helps reduce overall portfolio risk.
- As the book emphasizes, the correlation coefficient’s value will dramatically affect whether the new asset adds or subtracts from the portfolio’s volatility.
Utility: Allows investors to quantify the risk level of their portfolio, taking into account diversification benefits.
- It does however, become unwieldy with many terms.
Important Implications:
- Diversification and lower correlation - these factors are useful for any potential investor who wants a portfolio that is well-diversified and as "immune" to market shifts as possible.
- A portfolio with all its securities positively correlated cannot be easily helped.
In summary, portfolio analysis provides the tools to quantify the risk and return characteristics of a portfolio. It helps investors understand the potential trade-offs between risk and reward and to construct portfolios that are aligned with their investment goals and risk tolerance.

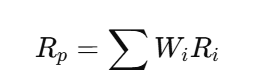
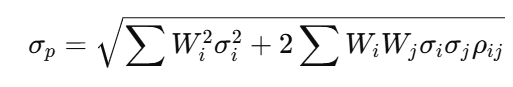
No Comments