Skip to main content

Time Value of Money

The Time Value of Money (TVM) is a fundamental financial concept stating that a dollar today is worth more than a dollar in the future. This is because money today can be invested to earn returns, whereas money received later loses potential earnings over time. The rationale behind TVM lies in factors such as inflation, risk, and opportunity cost.

For example, if you receive $1,000 today and invest it at an annual interest rate of 10%, it will grow to $1,100 in a year. However, if you receive that 1,000 one year later, you miss out on the opportunity to earn that extra 100. This principle underlies key financial decisions like investment analysis, loan calculations, and capital budgeting.

Compounding and Discounting – Future and Present Value

1. Compounding to Obtain Future Value (FV)

Compounding refers to the process of growing an investment by reinvesting earned interest. The future value of an investment depends on three factors:

  1. Initial Principal (P) – The starting amount of money.
  2. Interest Rate (r) – The rate at which money grows annually.
  3. Time Period (t) – The number of years the money is invested.

Formula for Future Value (FV):


Where:

  • FV = Future Value
  • P = Present Value (Initial Investment)
  • r = Interest Rate per Period
  • t = Number of Periods

For example, if you invest $1,000 at an annual interest rate of 10% for 3 years, the future value would be:
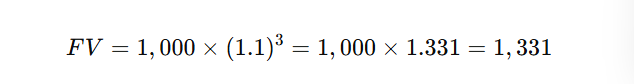Thus, after 3 years, the investment grows to $1,331.

Impact of Compounding Frequency

If interest is compounded more frequently (e.g., quarterly or daily), the future value increases. The formula for compound interest considering multiple periods per year is:

Where n is the number of compounding periods per year:

  • Annual (n = 1)
  • Semi-Annual (n = 2)
  • Quarterly (n = 4)
  • Monthly (n = 12)
  • Daily (n = 365)

For example, if $1,000 is invested at 10% compounded quarterly for 1 year:

By compounding quarterly instead of annually, the amount increases to $1,103.81 instead of $1,100, showing how frequent compounding benefits investors.

2. Discounting to Obtain Present Value (PV)

Discounting is the reverse of compounding. It determines the current worth of a future sum of money, given a discount rate. The present value tells us how much we need to invest today to reach a certain future amount.

Formula for Present Value (PV):

Where:

  • PV = Present Value
  • FV = Future Value
  • r = Discount Rate (Interest Rate)
  • t = Number of Time Periods

For example, if you need $1,331 in 3 years and the interest rate is 10%, the present value would be:

This means that 1,000 today is equivalent to $1,331 in three years at a 10% return rate.

Net Present Value (NPV) and Discounting Applications

  • Capital Budgeting – Evaluating investment projects by discounting future cash flows.
  • Loan Repayments – Determining how much needs to be set aside today to meet future obligations.
  • Bonds and Securities – Pricing fixed-income investments based on expected returns.

Key Takeaways

  1. Compounding helps money grow over time by reinvesting interest.
  2. Discounting helps determine how much a future amount is worth today.
  3. More frequent compounding results in higher future values.
  4. Understanding TVM helps in making better financial decisions, such as loan calculations, investments, and capital budgeting.
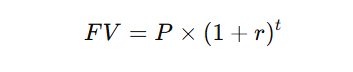
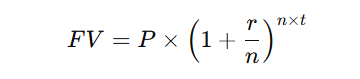
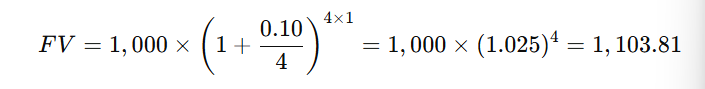
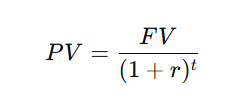
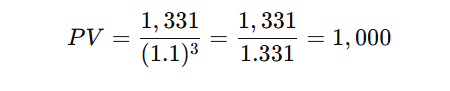
No Comments
Back to top