Option Greeks
Understanding the Basics
Imagine you've bought an option contract. This contract gives you the right, but not the obligation, to buy (call option) or sell (put option) an asset at a specific price (strike price) by a certain date (expiration date). The price of your option changes based on several factors. The "Greeks" are like dials that tell you how sensitive your option's price is to changes in those factors.
Think of it like driving a car:
- The option price is the car's current position.
- The Greeks are the steering wheel, gas pedal, and brakes – they tell you how the car will react to different inputs.
Here are the main Greeks explained simply, with their formulas:
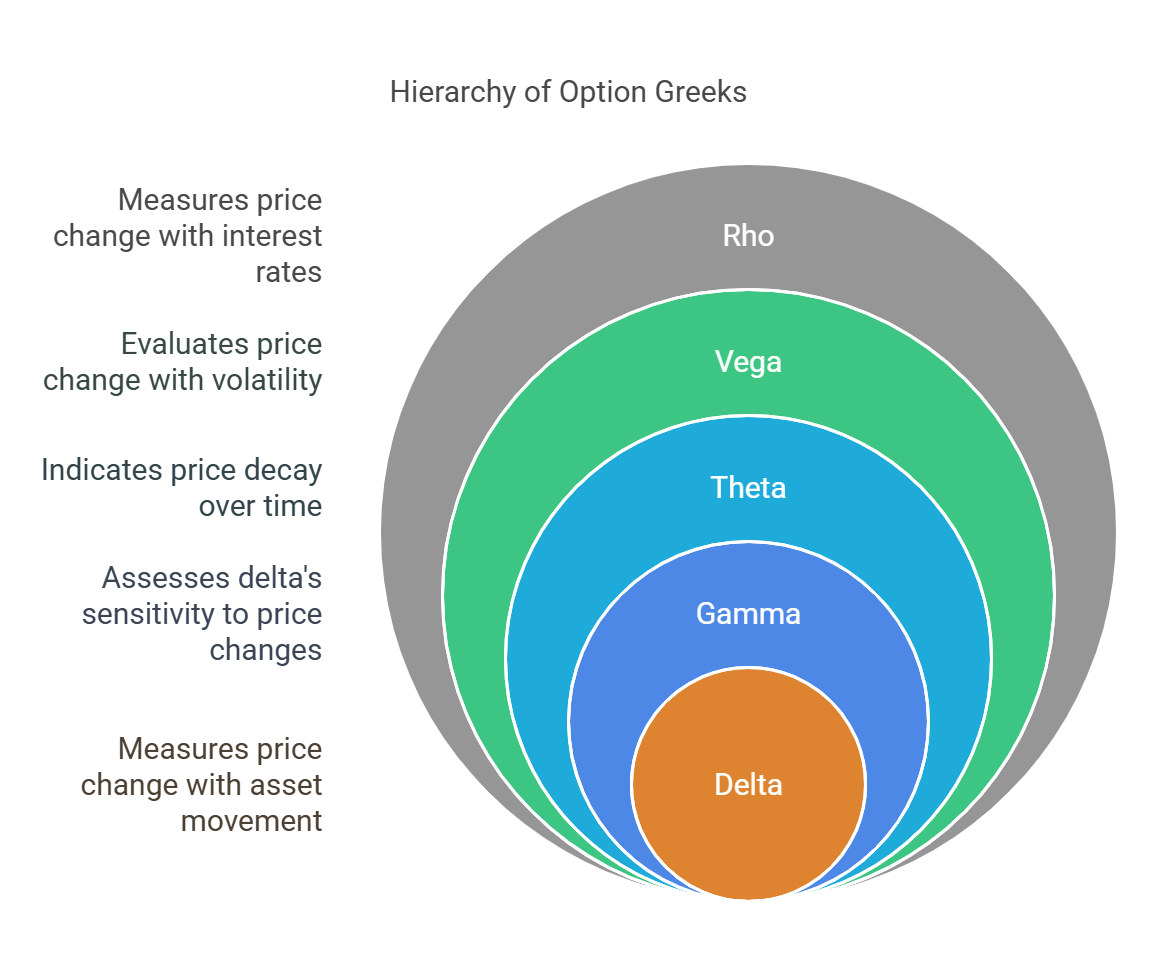 1. Delta (Δ) - The Steering Wheel:
1. Delta (Δ) - The Steering Wheel:
- What it tells you: How much the option price will move for every $1 move in the price of the underlying asset (e.g., the stock).
- Example: If a call option has a delta of 0.60, it means that for every $1 the stock price goes up, the option price will likely go up by $0.60.
- Call Options: Delta is always between 0 and 1.
- Put Options: Delta is always between -1 and 0.
-
Formula (Stock Option, No Dividend):
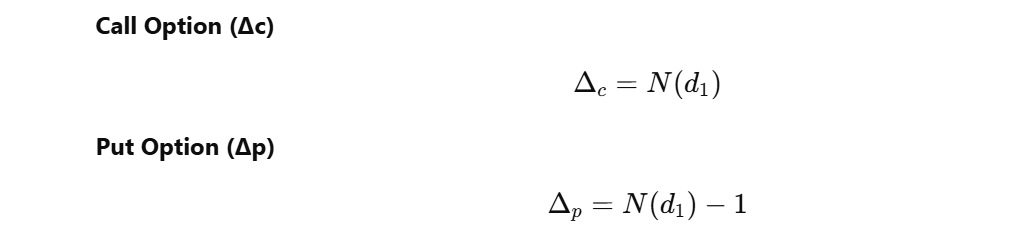
-
Formula (Stock Option, with Dividend):
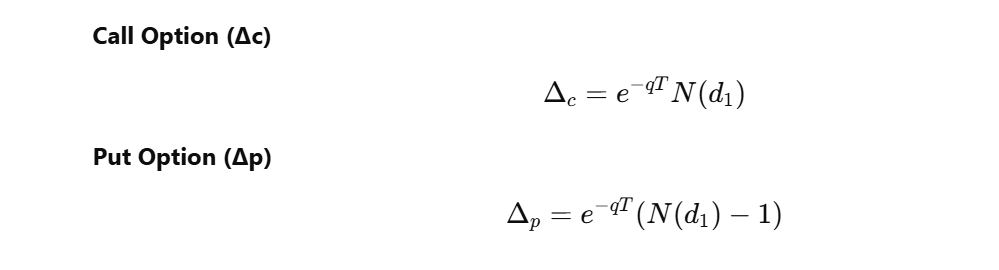 Where q is the continuous dividend yield (expressed as a decimal, e.g., 2% dividend yield is q = 0.02).
Where q is the continuous dividend yield (expressed as a decimal, e.g., 2% dividend yield is q = 0.02).
-
Formula (Currency Option):
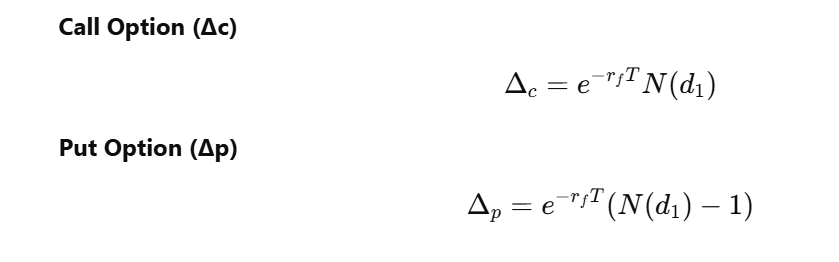 Where rf is the foreign risk-free rate.
Where rf is the foreign risk-free rate.
- Why it matters: Delta helps you understand how exposed your option is to price changes in the underlying asset.
2. Gamma (Γ) - The Sensitivity of the Steering Wheel:
- What it tells you: How much the delta will change for every $1 move in the underlying asset's price. It's like how sensitive the steering wheel is. If Gamma is high, even a small turn of the steering wheel (change in stock price) causes a big change in direction (delta).
- Example: If an option has a gamma of 0.10, and the stock price goes up by $1, the delta of the option will increase by 0.10.
- Always Positive (mostly): Gamma is positive for both calls and puts, meaning delta always moves in the same direction as the underlying asset.
-
Formula (Stock and Currency Options):
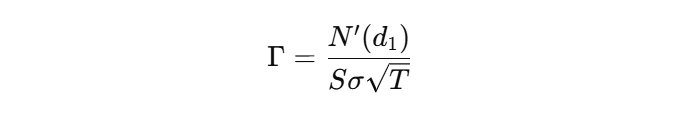
- Why it matters: Gamma helps you anticipate how your delta exposure will change as the stock price moves. This is crucial for managing risk, especially when you want to keep your portfolio delta-neutral (explained later).
3. Theta (Θ) - The Time Decay Clock:
- What it tells you: How much the option price will decrease each day as time passes. Options are "wasting assets" because they lose value as they approach their expiration date.
- Example: If an option has a theta of -0.05, it means the option price will decrease by $0.05 each day, all else being equal.
- Almost Always Negative: Theta is usually negative because options lose value as time goes by.
-
Formula (Stock Option, No Dividend - approximation):
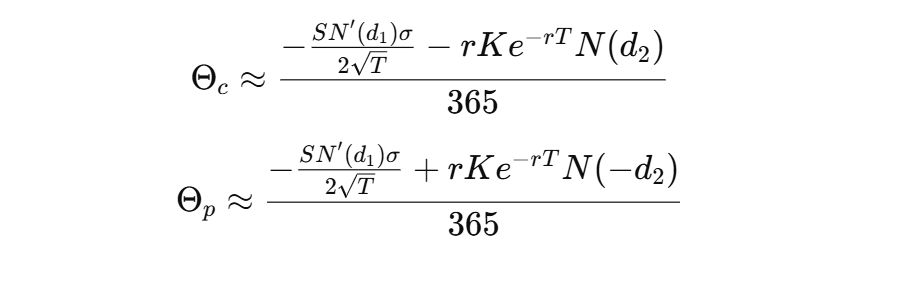
- Formula (Currency Option - approximation):
- Why it matters: Theta highlights the cost of holding options over time. You need the underlying asset to move in your favor quickly enough to offset the time decay.
4. Vega (ν) - The Volatility Meter:
- What it tells you: How much the option price will change for every 1% change in the implied volatility of the underlying asset. Implied volatility is a measure of how much the market expects the stock price to fluctuate.
- Example: If an option has a vega of 0.20, it means that if implied volatility increases by 1%, the option price will increase by $0.20.
- Always Positive: Vega is positive for both calls and puts because higher volatility makes options more valuable (there's a greater chance of a big payout).
- Formula (Stock and Currency Options):
- Why it matters: Vega helps you understand how exposed your option is to changes in market uncertainty.
5. Rho (ρ) - The Interest Rate Thermometer:
- What it tells you: How much the option price will change for every 1% change in the risk-free interest rate.
- Example: If a call option has a rho of 0.08, it means that if the risk-free interest rate increases by 1%, the option price will increase by $0.08.
- Calls: Positive Rho (higher interest rates increase call option value).
- Puts: Negative Rho (higher interest rates decrease put option value).
-
Formula (Stock Option, No Dividend):
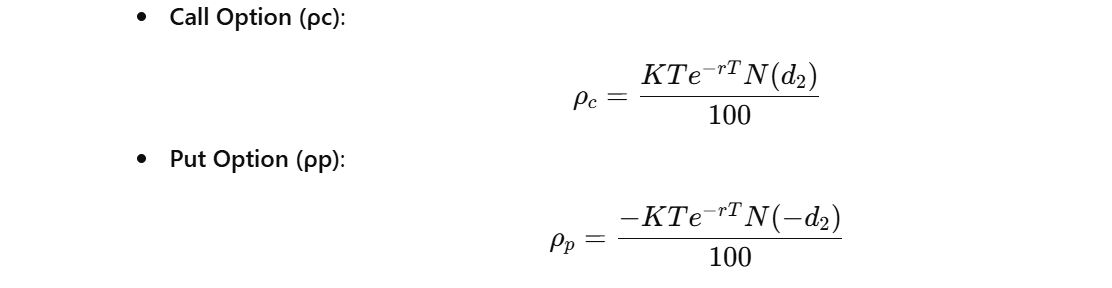
-
Formula (Currency Option):
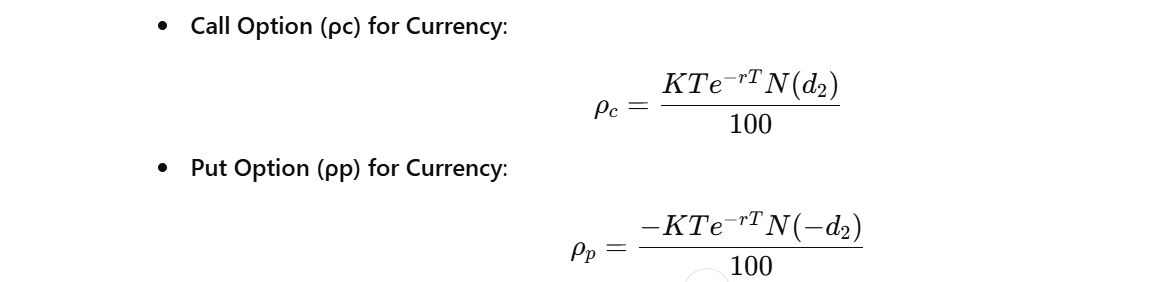
- Why it matters: Interest rates usually have a smaller impact on short-term options but can be more significant for longer-term options.
Key to Understanding the Formulas:
- S: Current price of the underlying asset (e.g., stock price)
- K: Strike price of the option
- T: Time to expiration (expressed in years)
- r: Risk-free interest rate (expressed as a decimal)
- σ (sigma): Volatility of the underlying asset (expressed as a decimal)
- q: Continuous dividend yield (expressed as a decimal)
- r_f: Foreign risk-free rate (expressed as a decimal)
- r_d: Domestic risk-free rate (expressed as a decimal)
- N(x): Cumulative standard normal distribution function (you can use a calculator or spreadsheet to find this value)
- N'(x): Standard normal probability density function (you can use a calculator or spreadsheet to find this value)
-
d1 & d2: Intermediate variables used in the Black-Scholes model:
- d1 = [ln(S/K) + (r + (σ^2)/2) * T] / (σ * √T)
- d2 = d1 - σ * √T
Important Considerations:
- Dividends: If the underlying stock pays dividends, it affects the option prices and the calculations of the Greeks (especially Delta).
- Currency Options: Currency options are similar, but instead of a stock, the underlying asset is a currency exchange rate. The formulas are adjusted to take into account the interest rates in both countries.
- The Black-Scholes Model is a Simplification: The Black-Scholes model makes certain assumptions that may not always hold true in the real world. Therefore, the calculated Greeks are just estimates, not guarantees. The formulas marked with "approximation" are simplified versions for illustrative purposes. More precise calculations may be required in practice.
In summary: The Greeks are essential tools for understanding and managing the risks associated with options trading. They help you quantify how sensitive your option positions are to various market factors. The formulas provide a more precise way to calculate these sensitivities.

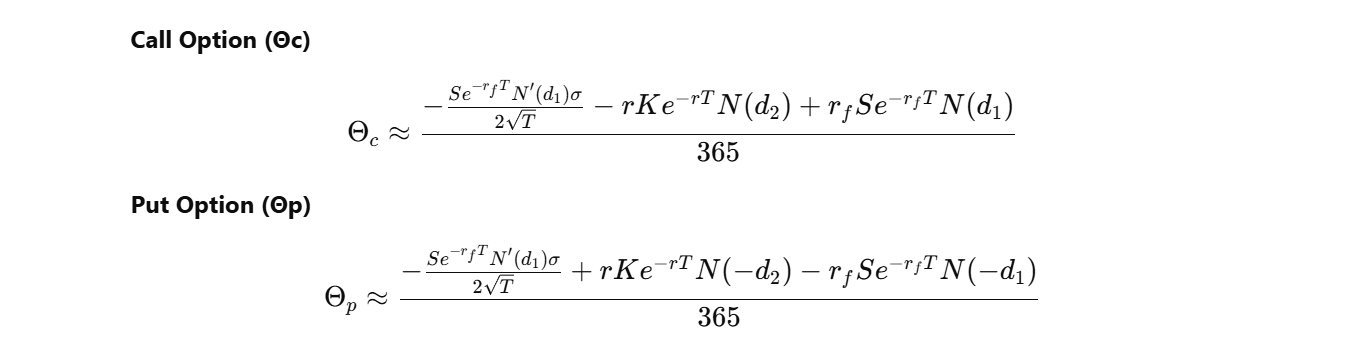
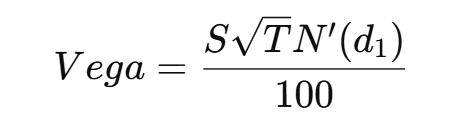
No Comments