Estimation of GARCH Models
The estimation of GARCH (Generalized Autoregressive Conditional Heteroskedasticity) models involves finding the values of the model’s parameters that best fit the observed financial time series data. This is usually achieved through Maximum Likelihood Estimation (MLE).
Maximum Likelihood Estimation (MLE)
MLE is a method of estimating the parameters of a model by maximizing the likelihood function. The likelihood function represents the probability of observing the data given a specific set of model parameters. The parameter values that maximize this function are known as the maximum likelihood estimates.
Steps in Estimating GARCH Models using MLE
1. Specify the Model:
You begin by specifying the GARCH model. A common model is
You may also specify the distribution of the error term ( z_t ), such as a normal distribution or t-distribution.
2. Formulate the Likelihood Function:
The likelihood function is based on the probability density function (PDF) of the error term. If we assume that the error term follows a normal distribution, the PDF is:

3. Formulate the Log-Likelihood Function:
To simplify calculations, the log-likelihood function is used. The log-likelihood function is the natural logarithm of the likelihood function:
4. Maximize the Log-Likelihood Function:
The goal is to find the parameter values ( \theta ) that maximize the log-likelihood function. This is typically done using numerical optimization algorithms like:
- Newton-Raphson (a second-order optimization algorithm),
- Broyden-Fletcher-Goldfarb-Shanno (BFGS),
- Nelder-Mead (a simplex method for multidimensional optimization).
These algorithms iteratively adjust the parameter values to find the maximum.
5. Check for Convergence:
After applying the optimization algorithms, check if the solution has converged. If the optimization algorithm has not converged, you may need to adjust the starting values or constraints.
6. Calculate Standard Errors:
Once the parameters have been estimated, calculate their standard errors. The standard errors are derived from the Hessian matrix, which is the matrix of second-order partial derivatives of the log-likelihood function.
7. Perform Diagnostic Checks:
Finally, perform diagnostic checks to evaluate the model’s adequacy:
-
Residual Analysis: The residuals (standardized errors ( \frac{\varepsilon_t}{\sigma_t} )) should resemble white noise. You can check their autocorrelation (ACF) and partial autocorrelation (PACF) functions to ensure no autocorrelation remains.
-
Ljung-Box Test: A statistical test for autocorrelation in the residuals.
-
Normality Tests: Check the standardized residuals for deviations from normality (using tests like the Jarque-Bera test).
Considerations in Estimation
Conclusion
Estimating GARCH models involves specifying the model, formulating the likelihood function, and maximizing it using numerical optimization methods. The method of Maximum Likelihood Estimation (MLE) is typically used to estimate the parameters, and tools like R and Python provide efficient ways to perform this estimation. After estimating the model, it’s crucial to perform diagnostic checks to assess its adequacy and robustness.


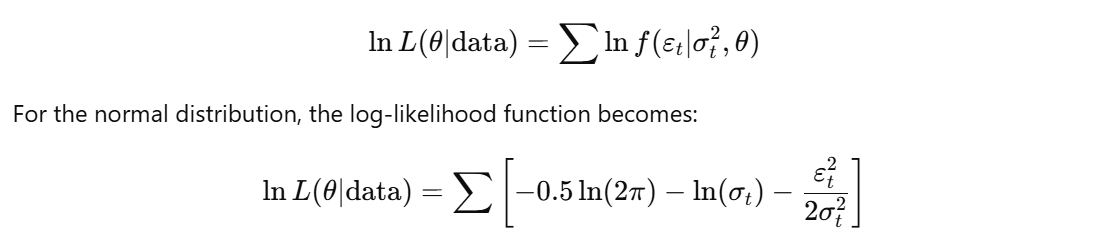

No Comments