Performance Evaluation of Managed Funds
Sharpe, Treynor, and Jensen's Measures
Core Concept: Evaluating the performance of managed funds is crucial for investors to assess whether the fund is delivering satisfactory returns relative to the risk taken. Sharpe, Treynor, and Jensen's measures are popular risk-adjusted performance measures used to evaluate managed funds.
Key Principles:
- Risk-Adjusted Return: These measures evaluate returns in relation to the risk taken to achieve those returns.
- Benchmarking: The fund's performance is compared to a benchmark index or a risk-free rate of return.
1. Sharpe Ratio
-
Definition: The Sharpe Ratio measures the risk-adjusted return of an investment portfolio by calculating the excess return per unit of total risk.
-
Formula:
Sharpe Ratio = (Rp - Rf) / σp- Where:
-
Rp= Average return of the portfolio -
Rf= Risk-free rate of return -
σp= Standard deviation of the portfolio (total risk)
-
- Where:
-
Interpretation:
- Higher Sharpe Ratio: Indicates a better risk-adjusted performance. It means the fund is generating more excess return for each unit of total risk.
- Lower Sharpe Ratio: Indicates a worse risk-adjusted performance.
- Sharpe Ratio > 1: Generally considered good.
- Sharpe Ratio > 2: Considered very good.
- Sharpe Ratio > 3: Considered excellent.
-
Example:
- Fund A: Rp = 15%, Rf = 3%, σp = 10%
- Sharpe Ratio = (15% - 3%) / 10% = 1.2
- Fund B: Rp = 20%, Rf = 3%, σp = 15%
- Sharpe Ratio = (20% - 3%) / 15% = 1.13
- Interpretation: Even though Fund B has a higher return, Fund A has a better risk-adjusted performance because it has a higher Sharpe Ratio.
- Fund A: Rp = 15%, Rf = 3%, σp = 10%
-
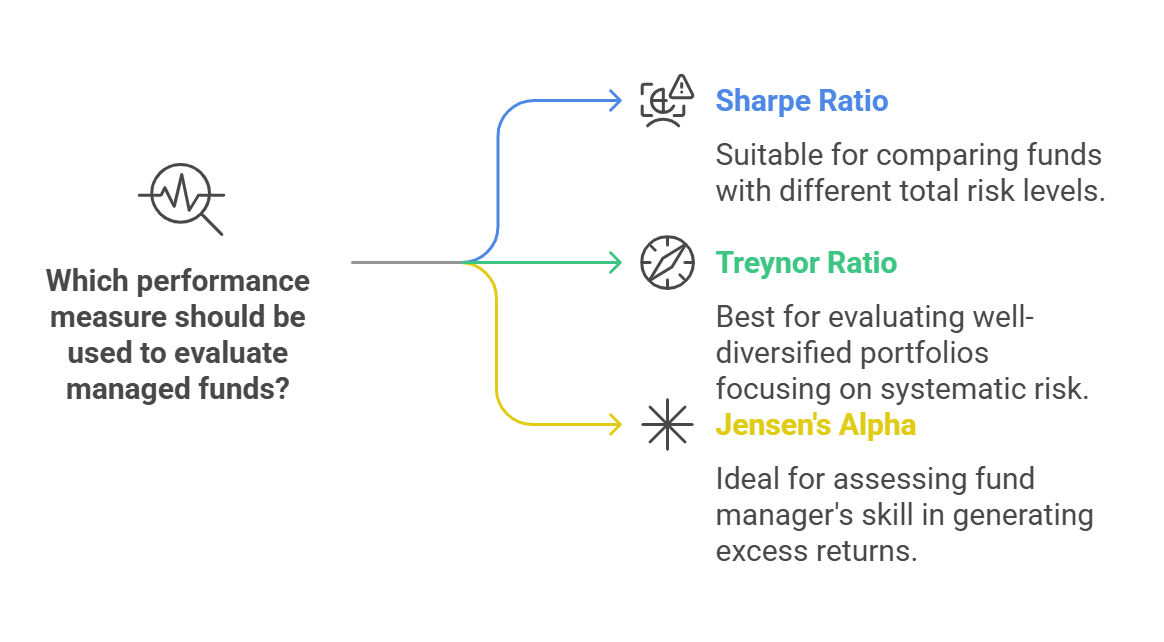
Usefulness: The Sharpe Ratio is useful for comparing the risk-adjusted performance of funds with different levels of risk.
-
Limitations:
- The Sharpe Ratio uses standard deviation as a measure of risk, which assumes that returns are normally distributed. This may not always be the case.
- The Sharpe Ratio is sensitive to the choice of the risk-free rate.
2. Treynor Ratio
-
Definition: The Treynor Ratio measures the risk-adjusted return of an investment portfolio by calculating the excess return per unit of systematic risk (beta).
-
Formula:
Treynor Ratio = (Rp - Rf) / βp- Where:
-
Rp= Average return of the portfolio -
Rf= Risk-free rate of return -
βp= Beta of the portfolio (systematic risk)
-
- Where:
-
Interpretation:
- Higher Treynor Ratio: Indicates a better risk-adjusted performance. It means the fund is generating more excess return for each unit of systematic risk.
- Lower Treynor Ratio: Indicates a worse risk-adjusted performance.
-
Example:
- Fund C: Rp = 14%, Rf = 3%, βp = 0.8
- Treynor Ratio = (14% - 3%) / 0.8 = 13.75%
- Fund D: Rp = 16%, Rf = 3%, βp = 1.2
- Treynor Ratio = (16% - 3%) / 1.2 = 10.83%
- Interpretation: Even though Fund D has a higher return, Fund C has a better risk-adjusted performance because it has a higher Treynor Ratio.
- Fund C: Rp = 14%, Rf = 3%, βp = 0.8
-
Usefulness: The Treynor Ratio is useful for evaluating the performance of well-diversified portfolios, where systematic risk is the primary concern.
-
Limitations:
- The Treynor Ratio uses beta as a measure of risk, which may not be accurate if the portfolio is not well-diversified.
- The Treynor Ratio is sensitive to the choice of the risk-free rate.
3. Jensen's Alpha
-
Definition: Jensen's Alpha measures the excess return of a portfolio relative to its expected return based on the Capital Asset Pricing Model (CAPM). It represents the value added by the fund manager's skill.
-
Formula:
Jensen's Alpha = Rp - [Rf + βp * (Rm - Rf)]- Where:
-
Rp= Average return of the portfolio -
Rf= Risk-free rate of return -
βp= Beta of the portfolio -
Rm= Average return of the market portfolio -
[Rf + βp * (Rm - Rf)]= Expected return of the portfolio based on CAPM
-
- Where:
-
Interpretation:
- Positive Jensen's Alpha: Indicates that the fund has outperformed its expected return based on the CAPM, suggesting that the fund manager has added value.
- Negative Jensen's Alpha: Indicates that the fund has underperformed its expected return based on the CAPM, suggesting that the fund manager has detracted value.
- Zero Jensen's Alpha: Indicates that the fund has performed as expected based on the CAPM.
-
Example:
- Fund E: Rp = 13%, Rf = 3%, βp = 0.9, Rm = 11%
- Jensen's Alpha = 13% - [3% + 0.9 * (11% - 3%)] = 13% - [3% + 0.9 * 8%] = 13% - 10.2% = 2.8%
- Fund F: Rp = 10%, Rf = 3%, βp = 0.7, Rm = 11%
- Jensen's Alpha = 10% - [3% + 0.7 * (11% - 3%)] = 10% - [3% + 0.7 * 8%] = 10% - 8.6% = 1.4%
- Interpretation: Fund E has a higher Jensen's Alpha than Fund F, indicating that it has added more value relative to its expected return based on the CAPM.
- Fund E: Rp = 13%, Rf = 3%, βp = 0.9, Rm = 11%
-
Usefulness: Jensen's Alpha is useful for evaluating the skill of the fund manager in generating excess returns.
-
Limitations:
- Jensen's Alpha relies on the CAPM, which has several assumptions that may not hold true in the real world.
- Jensen's Alpha may not accurately reflect the fund manager's skill if the fund's investment strategy deviates significantly from the market portfolio.
Summary Table:
| Measure | Formula | Risk Measure Used | Usefulness | Limitations |
|---|---|---|---|---|
| Sharpe Ratio | (Rp - Rf) / σp | Total Risk (σp) | Comparing funds with different levels of total risk. | Assumes normal distribution of returns, sensitive to choice of Rf. |
| Treynor Ratio | (Rp - Rf) / βp | Systematic Risk (βp) | Evaluating well-diversified portfolios. | Assumes well-diversified portfolio, sensitive to choice of Rf. |
| Jensen's Alpha | Rp - [Rf + βp * (Rm - Rf)] | CAPM's Expected Return | Evaluating fund manager's skill in generating excess returns relative to the CAPM. | Relies on CAPM assumptions, may not be accurate for funds with strategies deviating from the market portfolio. |
Sharpe, Treynor, and Jensen's measures are valuable tools for evaluating the performance of managed funds. Each measure provides a different perspective on risk-adjusted returns, and it's important to consider all three measures (along with other factors) when assessing a fund's performance.

No Comments