Law of Large Numbers and Characteristics of an Ideally Insurable Risk

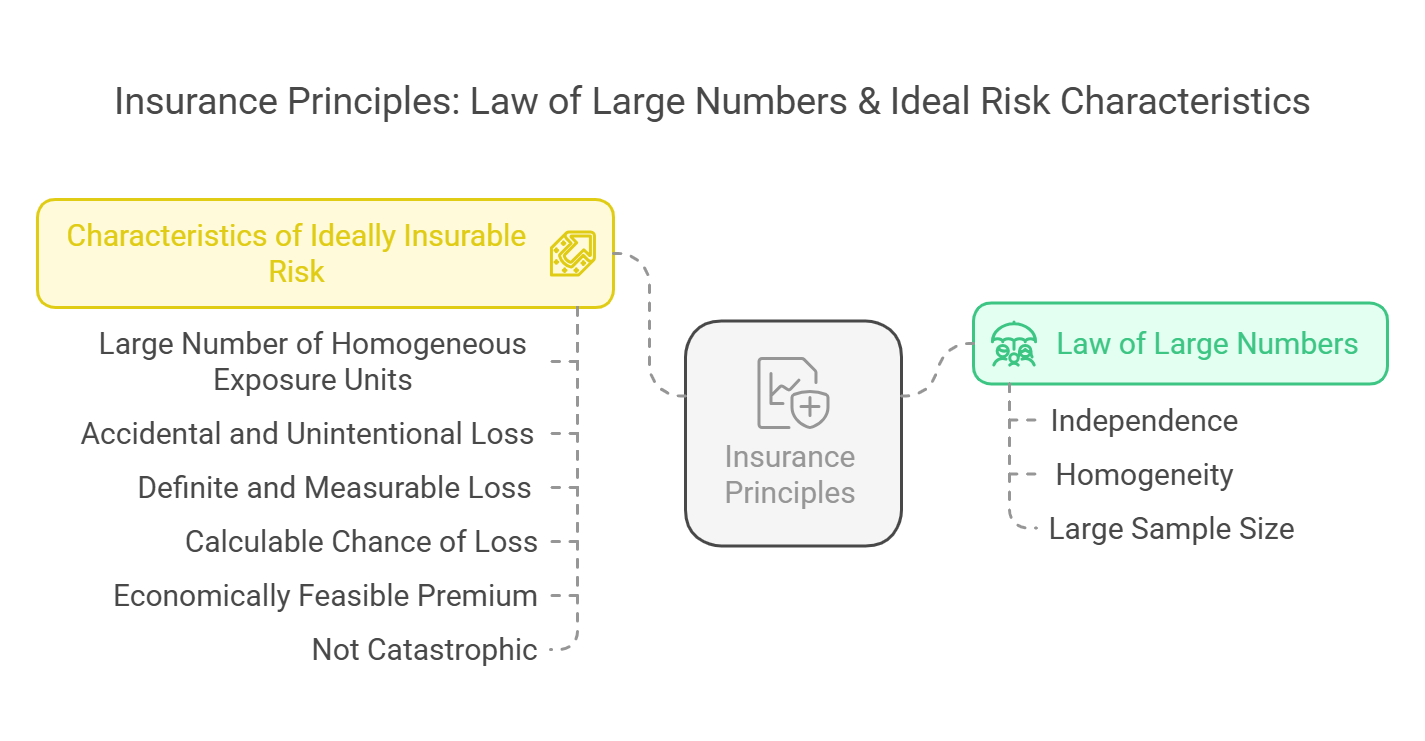
I. Law of Large Numbers:

• Definition: The Law of Large Numbers (LLN) is a statistical principle stating that as the number of independent and identically distributed observations increases, the average of these observations will converge towards the true expected value (or population mean). In simpler terms, the more data you have, the more reliable your estimates become.

• Application to Insurance: In insurance, the LLN is fundamental to the ability of insurers to predict future losses with reasonable accuracy. By insuring a large number of similar risks (e.g., many homeowners against fire), insurers can use historical data to estimate the probability of a loss occurring within the insured group.

• Key Principles:

  • Independence: The risks being insured must be largely independent of each other. For example, insuring homes spread across a wide geographical area is preferable to insuring homes concentrated in an area prone to earthquakes.
  • Homogeneity: The risks should be relatively homogeneous, meaning they should have similar characteristics that affect the probability of loss. For example, insuring similar types of cars driven by similar age groups is preferable to insuring a mix of vehicles driven by a wide range of drivers.
  • Large Sample Size: The larger the number of insured risks, the more accurate the insurer's predictions will be. This allows insurers to spread the cost of losses over a larger premium base, making insurance more affordable.

• Impact on Insurer's Operations:

  • Predictability of Losses: Allows insurers to estimate future losses with a greater degree of confidence.
  • Premium Calculation: Enables insurers to set premiums that are sufficient to cover expected losses and expenses, while remaining competitive.
  • Solvency: Helps insurers maintain solvency (the ability to pay claims) by ensuring that losses are spread across a large group of policyholders.

II. Characteristics of an Ideally Insurable Risk:

For a risk to be ideally insurable, it should possess certain characteristics that allow insurers to accurately assess and manage the risk effectively. These characteristics are important for insurers to offer coverage at a reasonable price and remain financially stable.

• A. Large Number of Homogeneous Exposure Units:

  • Explanation: As discussed under the Law of Large Numbers, the insurer needs a large pool of similar risks to accurately predict losses. Homogeneity ensures that the risks have similar probabilities of loss.
  • Example: A large number of similar houses in a suburban area are easier to insure than a single unique building.

• B. Accidental and Unintentional Loss:

  • Explanation: The loss should be due to chance and outside the control of the insured. Intentional losses are not insurable because they create moral hazard.
  • Example: A fire caused by faulty wiring is insurable, but a fire intentionally set by the homeowner is not.

• C. Definite and Measurable Loss:

  • Explanation: The loss should be definite in terms of cause, time, place, and amount. It should be possible to verify that a loss has occurred and to accurately measure the amount of the loss.
  • Example: A car accident resulting in physical damage is a definite and measurable loss. Loss of reputation is often difficult to measure and may not be insurable.

• D. Calculable Chance of Loss:

  • Explanation: The insurer must be able to calculate the probability of loss with reasonable accuracy. This requires historical data and statistical analysis.
  • Example: Insuring against death is calculable because mortality rates are well-established. Insuring against the success of a new business venture is difficult to calculate.

• E. Economically Feasible Premium:

  • Explanation: The premium should be affordable for the insured, while still being sufficient to cover the insurer's expected losses and expenses. If the premium is too high, people will not purchase insurance.
  • Example: Insuring against a very rare but catastrophic event (e.g., being struck by a meteor) might require such a high premium that it is not economically feasible.

• F. Not Catastrophic:

  • Explanation: The risk should not be one that could cause a loss to a large number of insured units at the same time. Catastrophic events, such as widespread natural disasters, can overwhelm an insurer's ability to pay claims.
  • Example: Insuring homes against earthquakes in an area prone to earthquakes is difficult because a single earthquake could cause widespread damage. Insurers often use reinsurance to manage catastrophic risk. Adherence to these characteristics allows insurance companies to function effectively, providing financial protection to individuals and businesses while maintaining their own financial stability. Risks that deviate significantly from these characteristics may be difficult or impossible to insure privately.